Will Lake Mead go dry? - Solutions
These are the answers to the tutorial "Will Lake Mead go dry?".
Download the model and configuration files
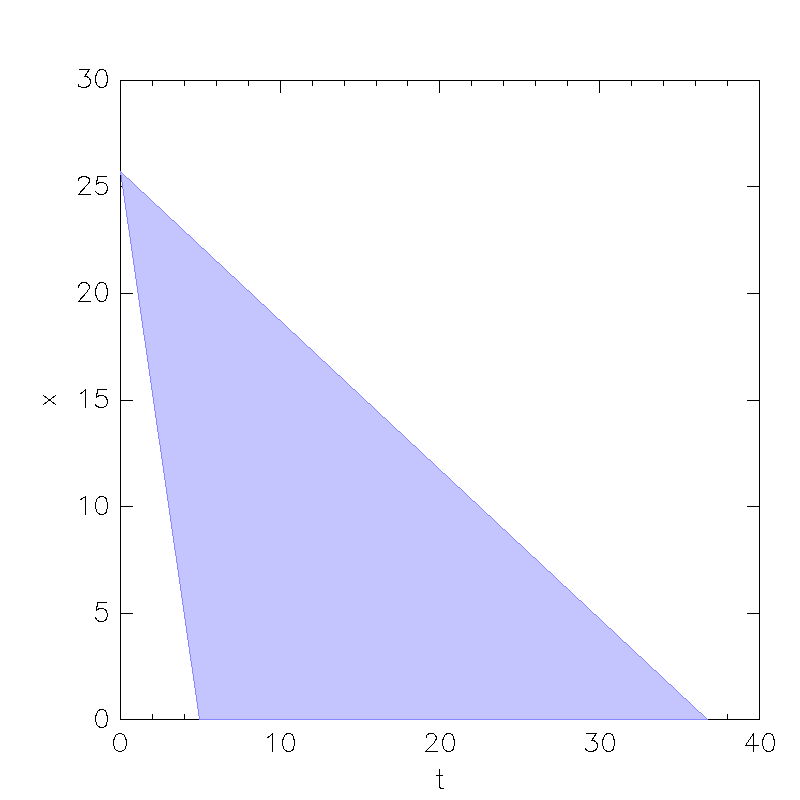
Constant Rate Model
A Solution: 1_lm.xml , 1_lm.cfg
a) In what time frame could Lake Mead be dry according to this model? What is the largest reachable value of t, and why is it finite?
According to this model, Lake Mead could be dry in ~ 5 to 39 years. T is finite because rout>rin at all times, so that the water level x is sinking constantly. So that after some finite amount of time, x will become negative, but there is no state which allows x < 0, which will cause time to stop.
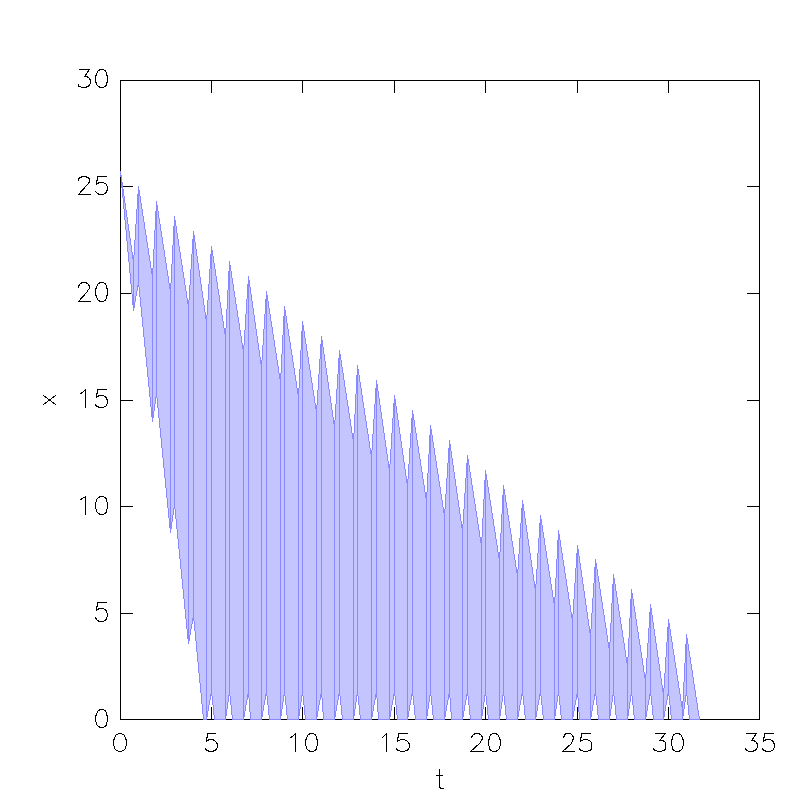
Switched Rate Model
A Solution: 2_lm.xml , 2_lm.cfg
b) In what time frame could Lake Mead be dry according to this model?
According to this model, Lake Mead could be dry in ~ 5 to 31 years.
c) At what values of t can transition rd take place?
The transition rd can take whenever t mod 1=0 . The guard of the transition ensures that c>=1, and the invariant c<=1 of the location 'rainy' imposes the jump on c=1. As c and t both start from 0 and have derivative 1, and as c is reset when it reaches c=1, we have c = t mod 1.
d) How can one model the transition from dry to rainy without a guard?
The guard of this transition can be added to the invariant of the location rainy. In order to jump from dry to rainy both the transition's guard and the target state's invariant must be satisfied, which allows us in this case to transfer the constraint into the invariant.
e) How can one model the transition from rainy to dry with a regular affine assignment instead of a reset?
We know that c=1 at the time of the transition (because the jump is forced). We may replace c'=0 with c'=c-1, which should have the same effect.
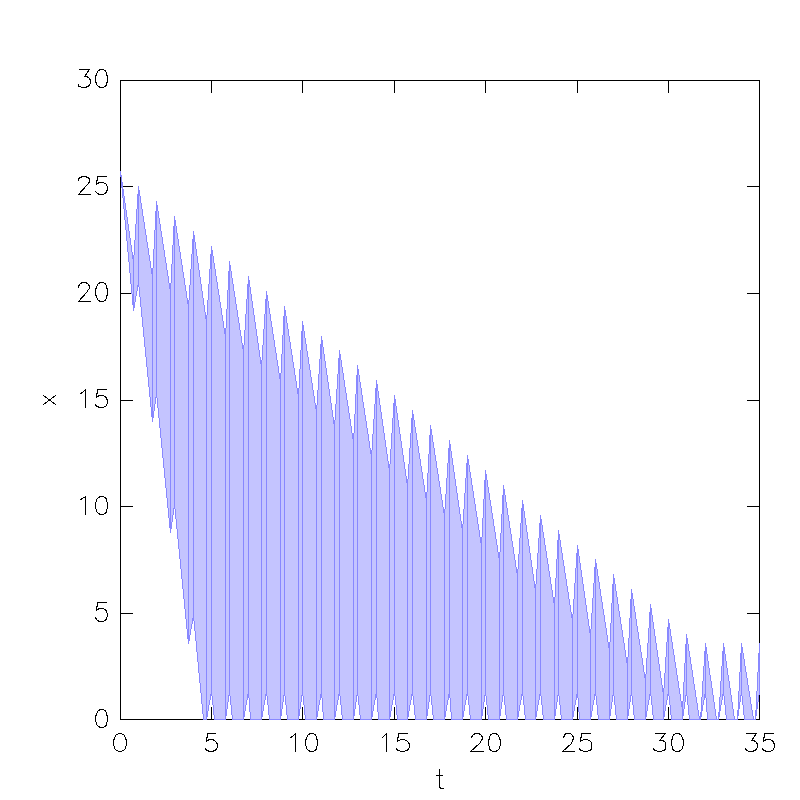
Another Solution (where time doesn't stop): 2b_lm.xml , 2b_lm.cfg
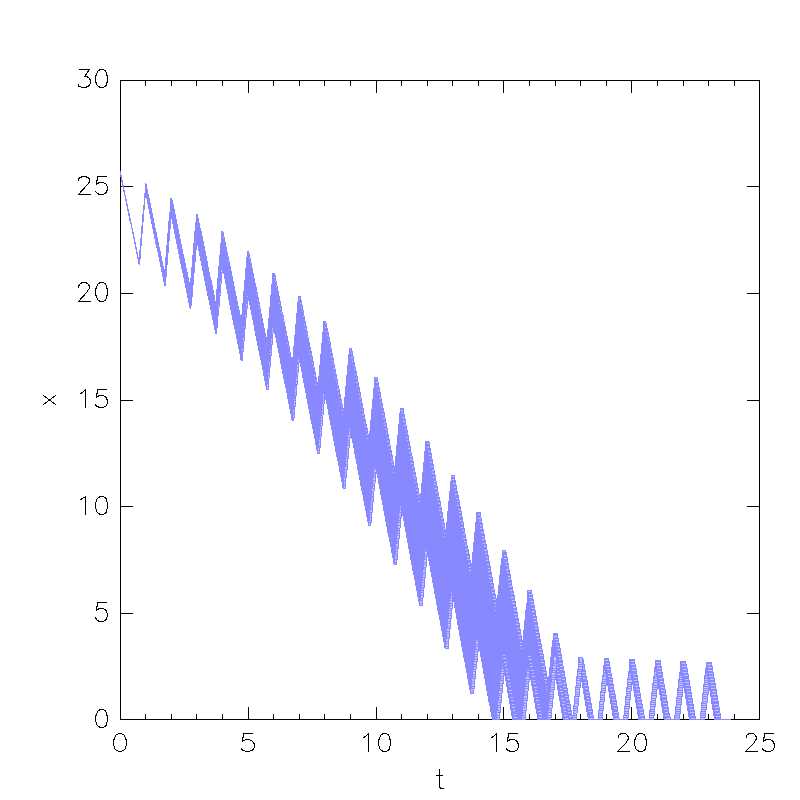
Model with Affine Continuous Dynamics
A Solution (where time doesn't stop): 3_lm.xml , 3_lm.cfg
f) In what time frame could Lake Mead be dry according to this model?
According to this model, Lake Mead could be dry (during the dry season) within 14-15 years, and after 18 years it would always be dry during the dry season.